イールドカーブと金利の期間構造
金利とディスカウントファクターについて、現在と10年後のみの比較をしたが、これは2年後、5年後、20年後のように様々な期間について考えることができる。すなわち、金利とディスカウントファクターは期間に関する関数と考えることができ、\(\small DF(T) \)や \(\small r(T) \)のように表すことができる。例えば、連続複利を用いれば、$$\small DF(T) = \exp(-r(T)T)$$と表現でき、金利とディスカウントファクターは1対1で対応するため、両者は同一視できる。
このように、期間の関数として表されたディスカウントファクターや金利のことをイールドカーブ(Yield Curve)という。期間にかかわらず金利が一定であるとは限らず、一般には短い期間と比較して長い期間の金利の方が高くなる傾向がある。イールドカーブの形状は金利の期間構造といわれ、右肩上がりのイールド カーブは順イールド、 右肩下がりのイールド カーブは逆イールドといわれる。 理論的な説明はおいおいしていくが、イールドカーブが逆イールドになることはあまりない。
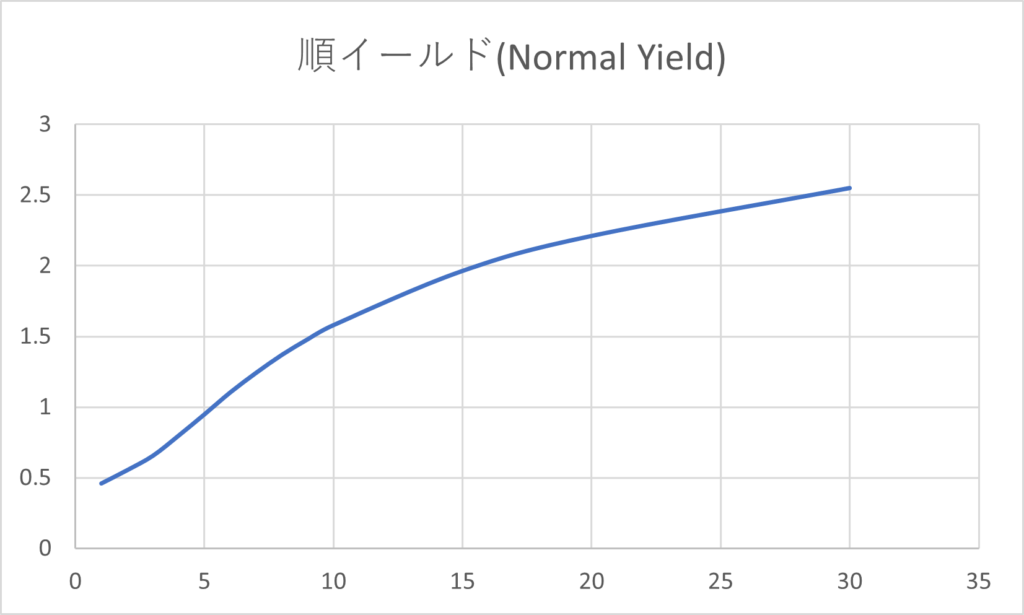
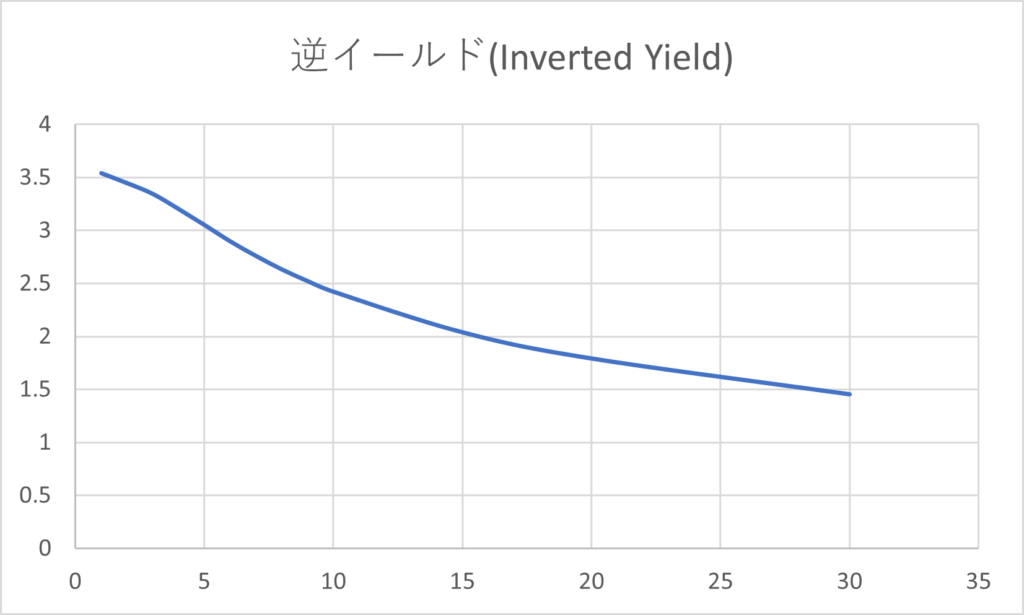
スポットレートとフォワードレート
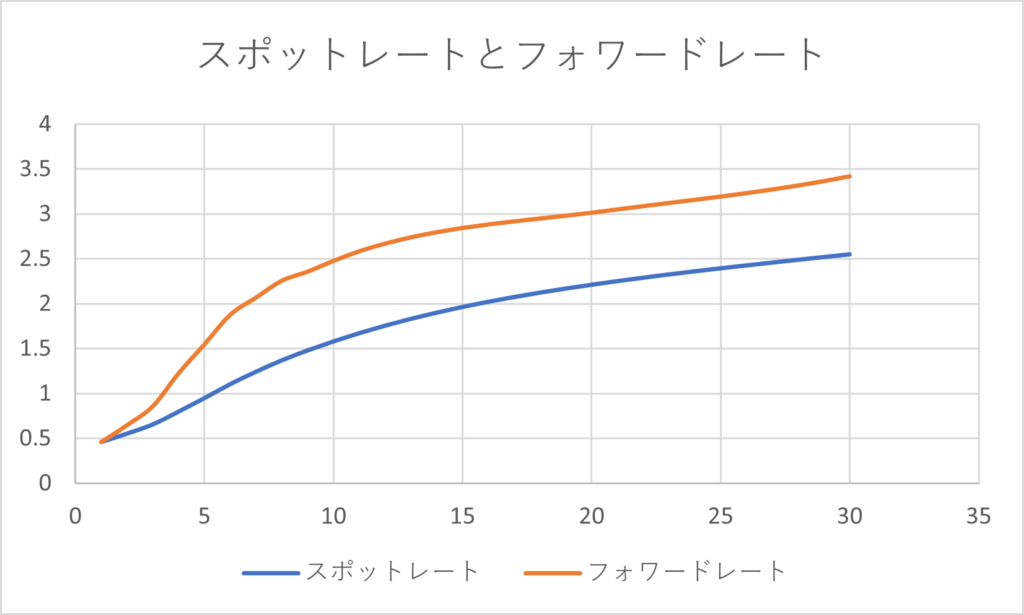
イールドカーブの表現方法にも2つ方法があり、 今日から1年後までの金利、今日から2年後までの金利、・・・のように今日からの期間を基準に金利を並べる方法と、 今日から1年後までの金利、 1年後から2年後までの金利、2年後から3年後までの金利、・・・というように一定の期間ごとに金利を並べる方法がある。前者のように今日を基準に期間を考える金利をスポットレート(Spot Rate)、一定の期間ごとに先日付を基準に期間を考える金利をフォワードレート(Forward Rate)という。
スポットレートが期間中の平均金利であるのに対して、フォワードレートは個別の期間の金利と考えることできる。フォワードレートはすぐに貸し出しを開始せず、1年後から1年間資金を貸し出すといった取引(先日付から開始する取引を今日行うことをフォワード取引(先渡取引)という。)の金利と考えることができる。それぞれのディスカウントファクターとの関係は以下のとおりである。$$\small r(T) = -\frac{\ln DF(T)}{T} \qquad \qquad \\ \small f(t,T) = -\frac{\ln DF(T) – \ln DF(t)}{T} $$グラフで見ると両者の違いは比較的理解しやすいだろう。
金利の期間計算方法
ここまで、期間というものを1年間であれば漠然と1と考えてきたが、実際の金利計算では期間の計算方法というものが定められている。代表的なものとして以下のようなものがある。
- ACT/365・・・実日数を365で割った値を期間とする。
- ACT/360・・・実日数を360で割った値を期間とする。
- 30/360,30E/360・・・1か月を30日とカウントし端の期間は実日数で足し合わせて、360で割った値を期間とする。
- ACT(NL)/365・・・うるう日を除いた実日数を365で割った値を期間とする。
ACT/365、ACT/360はインターバンク市場で用いられることが多く、30/360、30E/360は主に国債で用いられる。ACT(NL)/365は日本国債を市場で取引する際の利息計算に用いられる方式である。このような金利の期間計算方法はDay Count Conventionといい、計算した期間はDay Count Fractionという。金利と1口で言っても、その表現形式が単利なのか複利なのか、期間計算が何なのか、というところで種類が分かれるということになる。この期間計算方法には変種もあり、ブラジル(BRL)では営業日の日数を252で割って期間を計算するという方式(BUS/252)が、メキシコ(MXN)では1か月を28日で計算し、364で割って期間を計算するという方式(28/364)が用いられることもあるようである。ちなみに、28/364では1年を13か月として計算することになるのだが、どうやって計算するのだか。