公平なギャンブル
FXシミュレーターの栄ある第1弾はランダムウォーク(Random Walk)である。これは為替レートが上がる確率と下がる確率が同じであり、それ以前の結果が上がったか下がったかという結果から影響を受けずに毎回ランダムなサイコロに従って為替レートが変動するモデルである。どのような取引手法を用いようが結果の期待値に何の影響も及ぼさないという意味で、純粋で公平なギャンブルであるといえる。
為替レートがランダムウォークであるのならば、テクニカル分析を用いた取引手法を研究したり、情報を収集して分析したりすることにまったく意味がないし、長年の経験による学習にも意味がない。FXトレーダーの人たちから見たら、現実はこうであってほしくないと考える仮定の一つであろう。ちなみに、現実の市場の値動きがランダムウォークであり、それ以外のものであるべきでないとする仮説が効率的市場仮説である。
正規分布
ランダムな事象を表す確率分布として正規分布(Normal Distribution)といわれる確率分布がよく用いられる。これはランダムな値(乱数という。)をこの確率分布からサンプリングした場合に、その値が\(\small x \)である確率が$$\small f(x) = \frac{1}{\sqrt{2\pi}\sigma^2} \exp\left(\frac{(x-\mu)^2}{2\sigma^2}\right)$$である確率分布である。\(\small \mu \)は平均値、\(\small \sigma^2 \)は分散を表す。分散の平方根を標準偏差(Standard Deviation)というが、金融では一般に標準偏差のことをボラティリティ(Volatility)という。乱数\(\small x \)が平均\(\small \mu \)、分散\(\small \sigma^2 \)の正規分布に従うことは$$\small x \sim N(\mu, \sigma^2) $$と表現される。グラフにすると以下のとおりである。
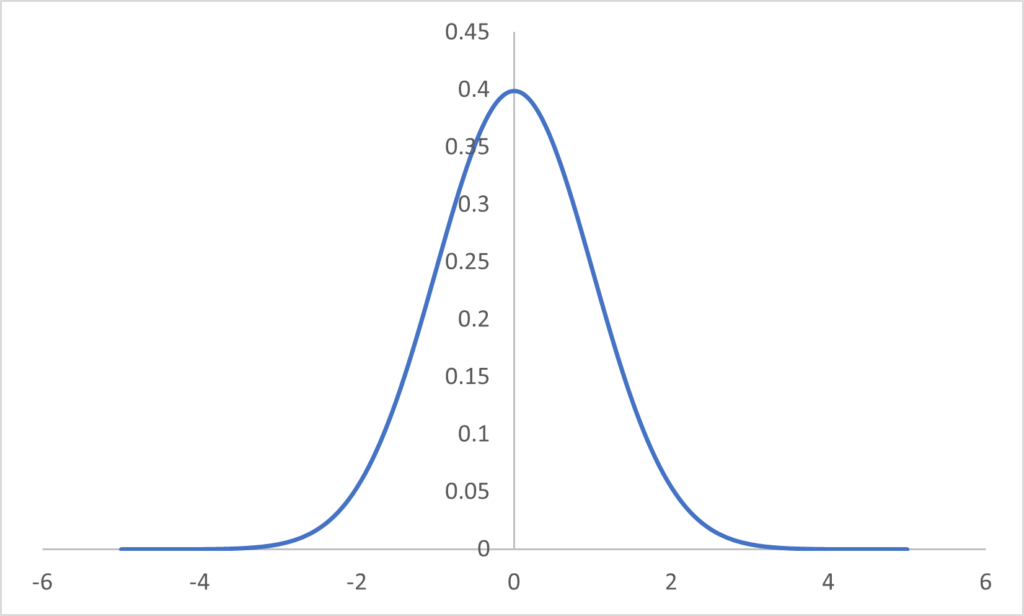
正規分布は、そのサンプリング値をいくら観測しても、サンプリング値の傾向に関する情報を引き出すことができないという意味で、最も情報量が少ない確率分布であり、ランダムな事象を取り扱う上で都合がよい確率分布といえる。金融やギャンブルで例えるならば、データをいくら解析しても利益を引き出すことができない確率分布ということになる。統計学では頻繁に登場する確率分布であり、金融や物理学でランダムな事象を扱う場合に必ずと言ってほど登場する確率分布である。
ランダムウォーク
時間の経過に応じて、直前の値に依存して確率的に値が変化するデータのことを時系列モデル、あるいは、確率過程という。ランダムウォークは時間経過による値の変化幅が正規分布に従う確率過程であり、以下のように表現される。$$\small x_t = x_{t-1} + \epsilon_t, \;\; \epsilon_t \sim N(0, \sigma^2) $$実際の経路を見てみると以下のようになり、ランダムな動きをしていることが見て取れるだろう。
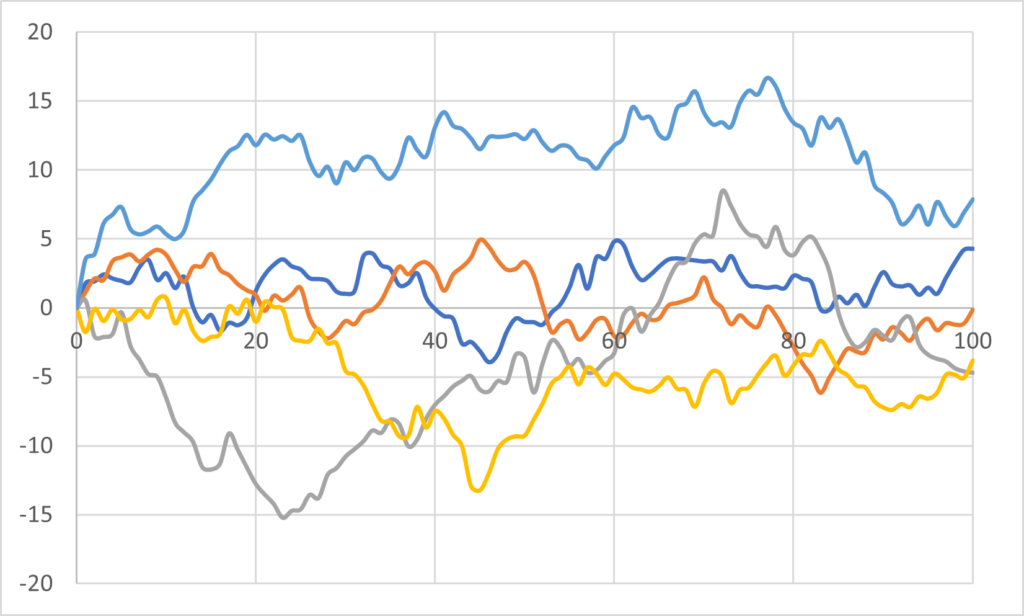
離散時間の確率過程として表現したが、連続時間のランダムウォークというものも存在して、数学ではブラウン運動(Brownian Motion)という。この場合、上記の式は、$$\small dX(t) = dB(t), \;\; B(t) \sim (0, \sigma^2t)$$という形で表される。実際に計算するとわかる通り、\(\small \frac{dX(t)}{dt} = \lim_{\Delta t \rightarrow 0} \frac{x(t+\Delta t) – x(t)}{\Delta t} = \frac{\epsilon_t}{\Delta t} \rightarrow \infty \)となり、時間に関する微分が定義できないため、上記の式に数学的な意味を持たせるということは容易ではない。連続時間の確率過程は数学的に取り扱いが難しいものなので、このブログでは扱わないがブラウン運動と言っている個所があった場合、ランダムウォークのことを言っていると考えてほしい。
モンテカルロシミュレーション
プログラムで疑似的な乱数を生成して、確率的なモデルをシミュレーションすることをモンテカルロシミュレーションという。実際にランダムウォークを為替レートに見立ててシミュレーションするシミュレーターを作ったので、トップメニューのランダムウォークという項目からページを開いて試してほしい。このシミュレーターで、”こんなのチョロい、楽勝楽勝”とか、”こんなの無理、1回も勝てない”とか思うようであれば、それは勘違いであるとだけ指摘しておく。