FXトレーディングのための経済理論

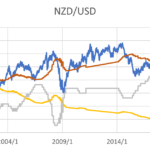
金利平価説(その５)

金利平価説の成立の可否に関しては1回目とほぼ同様の結論であると考えられるだろう。中央銀行は市場の動きを読みながら金融政策を考えるし、反対に市場側も中央銀行の動きを読みながら取引をしている部分もあるという点で、一貫した傾向を見出すことは難しいように見える。

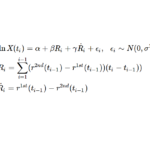
金利平価説について計算式通りに検証したが、もう少し改良の余地があるんじゃねえの？とおそらく思っただろう。AUDやNZDの表などを見れば、為替レートと金利差は連動性があるように見えるのだが、金利平価説の式によるフィッティングはそれをほとんど取り入れていないように見える。

BISの為替レートと政策金利のデータ(1999/01/01～2021/06/30、IDRのみ2006/01/01 ～2021/06/30 )を用いてエマージング通貨について回帰分析した結果とグラフは以下のとおりである。

通貨の傾向として、CHF,GBP,JPYは金利平価説よりの推定値であるが１とは乖離がある数値であるといえる。AUD,NZDは金利平価説とはむしろ逆の傾向があり、キャリートレード向きの通貨であると考えることができる。

フォワード為替レートが将来時点Tにおけるスポット為替レートの期待値であるとする仮説を金利平価説(Interest Rate Parity Theory)という。

現実的な為替レートの値動きを再現したい場合に、ランダムウォークでは不十分な部分もあり、過去データを使ったシミュレーションをすることでよりリアリティのある価格の動きを作ることができるかもしれない。

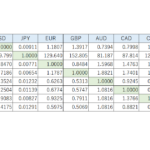
流動性の高い通貨ペアというのは大体限られており、任意の通貨ペアの価格データというのはそれらの合成から推定することになる。流動性が低かったり、取引自体がない通貨ペアの価格データなど必要なのかという疑問も生じるが、チャート等で比較したい場合もないわけではないだろう。

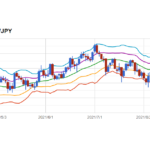
状態空間モデルとノンパラメトリックなアプローチとの大きな違いは、前者は将来の予測値を算出できることだろう。一般的なテクニカル分析が将来の予測値を算出することができないのは、アプローチとして内部の状態が法則性を持っていると仮定していないことによる。

もしかしたらテクニカル分析では、ツールの予測能力に大した意味はないのかもしれないと言ったが、それを扱わないことには何も始まらないので、一般的なテクニカル分析が何を推定、予測しているものなのかを定式化する。

デイトレードやスイングトレードといわれる期間が短い取引では、日々の値動きの特性や傾向を利用して利益の獲得を目指す戦略がとられる。この価格の動きの特性や傾向を抽出するための統計的な分析を総称してテクニカル分析といってよいだろう。