問題
テイラールールの説明でGDPギャップというものがHodrick Prescott(HP) Filterというものから推定されているらしい、ということを書いたがそれを紹介しようと思う。スプライン補間と異なるやり方として、観測されるデータにノイズが含まれているものと仮定として、元のデータを必ずしも通らない形で補間処理や予測処理を行うこともできる。こういった処理は一般に、フィルタリング(Filtering)といわれており、HP Filterはこのフィルタリングの1種と考えることができる。特に、観測したデータからノイズを取り除いて、過去における真の値を推定しようとすることを平滑化(スムージング)というが、HP Filterはこの平滑化に含まれる手法の一つと考えることができる。
GDPのような観測されるデータを\(\small y_1,y_2,\cdots, y_n \)と表すと、HP Filterの最適化問題は以下のように表される。$$\small \min_{u_1,u_2,\cdots,u_n} \sum_{i=1}^n (y_i-u_i)^2 + \lambda \sum_{i=2}^{n-1} (u_{i-1}-2u_{i}+u_{i+1})^2 $$ 第1項目は元のデータとの二乗誤差を最小化するという意味で最小二乗法と同じであるが、制約として第2項に傾き(1次微分)の変化率が可能な限り小さくなるように罰則項が追加されている。第2項がなければ、\(\small y_i=u_i \)であるが、この項があるために元のデータとは一致せず、滑らかな曲線になるということである。\(\small \lambda \)は平滑化の度合いを指定するパラメータであるが、Rule of Thumbとして、年次データの場合は\(\small \lambda=100 \)、四半期データの場合は \(\small \lambda=1600 \)、 月次データの場合は \(\small \lambda=14400 \)と設定するようである。
解法
例のごとく、目的関数を偏微分して0と置くことで解を求めることができる。面倒くさいが和のうち前後の添え字についても微分の対象に含む必要があり、\(\small 3 \leq i \leq n-2 \)の範囲では、以下のように計算できる。$$\small \frac{\partial F}{\partial u_i}=2(u_i-y_i) – 4 \lambda (u_{i-1}-2u_{i}+u_{i+1}) \qquad \qquad \qquad \qquad \\ \small + 2 \lambda (u_{i-2}-2u_{i-1}+u_{i}) + 2 \lambda (u_{i}-2u_{i+1}+u_{i+2}) = 0 $$ 整理すると $$\small y_i = u_i + \lambda (u_{i-2}-4u_{i-1}+6u_{i} -4u_{i+1}+u_{i+2})$$を得る。\(\small i=1,2,n-1,n \)についても同様に計算すると$$\small y_1 = u_1+\lambda(u_{1}-2u_{2}+u_{3}) \qquad \qquad \qquad \; \\ \small y_2 = u_2+\lambda(-2u_{1}+5u_{2}-4u_{3}+u_{4}) \qquad \;\;\; \\ \small y_{n-1} = u_2+\lambda(u_{n-3}-4u_{n-2}+5u_{n-1}-2u_{n}) \\ \small y_n = u_n+\lambda(u_{n-2}-2u_{n-1}+u_{n}) \qquad \qquad \; $$となる。
ここまでわかれば、連立方程式として表すことができて以下のようになる。 $$\scriptsize \left[ \begin{array}{ccccccccc} 1+\lambda&-2\lambda&\lambda&0&\cdots&0&0&0&0 \\ -2\lambda&1+5\lambda&-4\lambda &\lambda&\cdots&0&0&0&0 \\ \lambda&-4\lambda&1+6\lambda&-4\lambda&\cdots&0&0&0&0 \\ 0&\lambda&-4\lambda&1+6\lambda&\cdots&0&0&0&0 \\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\cdots&1+6\lambda&-4\lambda&\lambda&0\\ 0&0&0&0&\cdots&-4\lambda&1+6\lambda&-4\lambda&\lambda \\ 0&0&0&0&\cdots& \lambda&-4\lambda&1+5\lambda&-2\lambda \\ 0&0&0&0&\cdots&0&\lambda&-2\lambda&1+\lambda\\ \end{array} \right] \left[ \begin{array}{c} u_1\\ u_2\\ u_3\\ u_4\\ \vdots\\ u_{n-3}\\ u_{n-2}\\ u_{n-1}\\ u_{n}\\ \end{array} \right]=\left[ \begin{array}{c} y_1\\ y_2\\ y_3\\ y_4\\ \vdots\\ y_{n-3}\\ y_{n-2}\\ y_{n-1}\\ y_{n}\\ \end{array} \right]$$ この連立方程式を解けばよいのだが、LU分解や掃き出し法などで解こうとすると解が発散してしまうことが多い。重回帰分析で言えば、高い相関を持った多数の説明変数で回帰分析していることに近い処理をしているためだろう。そのため、計算する際は特異値分解を利用して解くと良いだろう。HP Filter用の収束計算によるアルゴリズムなどもいくつか存在するようである。
例
例として、日本のGDP(JPY)にHP Filterを適用して計算した例を示す。2010年のGDPを100とするように基準化しているが、原データに行列を掛けるだけであるため、基準化しなくても適用できることは容易にわかるだろう。図で表すと以下のとおりである。
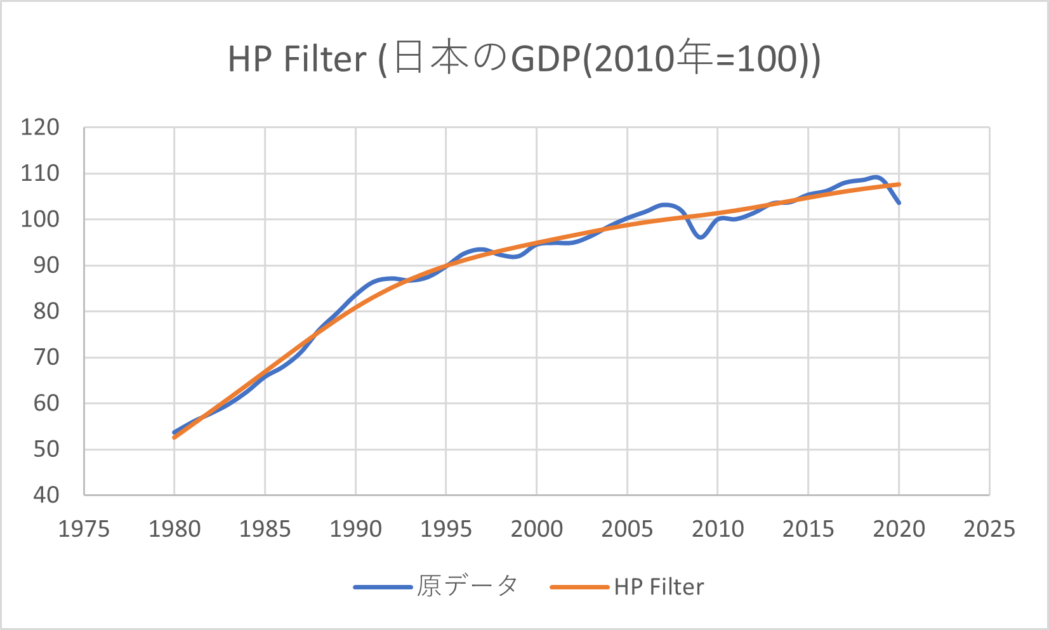
大体、中間の値を通っていることがわかる。テクニカル分析に例えると移動平均線に近く、GDPギャップは乖離率に相当するものであるかもしれない。計量経済学の人たちからはあまり評判の良い手法ではないが、手早くノイズをカットしたいという場合には利用しやすい手法であろうと思われる。また、これを利用したテクニカル分析なども考えることができるかもしれない。