パターン認識－最近傍法－

最近傍法(Nearest Neighbor Rule)

　人間の学習で最もわかりやすい手法は丸暗記だろう。中間テストや期末テストの前の1夜漬けがこれに相当する。パターン認識においても類似の手法があり、観測されたパターン(過去問とその解答)をすべて記憶し、新たな条件 (実際のテストの問題)が与えられたときにその中から最も近いと考えられるデータ(解答)を引っ張り出す手法を最近傍法(Nearest Neighbor Rule)という。パターン認識のアルゴリズムの中では最も単純なアプローチといえるが、単純であるからこそ強力な部分もあって馬鹿にできないアルゴリズムである。

　最近傍法を適用する場合に重要になるのは、記憶されているパターンと新たに与えられたパターンの近さの基準(距離)をどのように定義するかだろう。わかりやすいのは、情報に重み付けをしてその二乗和を2つのパターンの距離として定義することだろう。$\small n $個のパラメータ$ \small x_1,x_2,\cdots, x_n $について、記憶されているパターンが$\small m $個$ \small (p_{1,1},\cdots,p_{1,n}), (p_{2,1},\cdots,p_{2,n}), \cdots,$ $ \small (p_{m,1},\cdots,p_{m,n}) $とそれに対応するカテゴリ(解答)$\small y_1,y_2,\cdots, y_m $がある場合に、距離を$$\small d(x, p_j) = \sum_{k=1}^n w_k (x_k-p_{j,k})^2$$のように定義して、この距離が最小となる$\small j^{\ast} $を探索して、$\small y_{j^{\ast}} $を解とすればよい。このような距離はユークリッド距離(Euclidian Distance)といわれる。他にもマンハッタン距離 $$\small d(x, p_j) = \sum_{k=1}^n w_k |x_k-p_{j,k}|$$やパターンの分散共分散を利用して重みを計算するマハラノビスの距離といったものを用いることもできる。

　当然のことながら、記憶しているパターンの中に近いものが存在しないという場合もある。一定の距離以上乖離した場合は、カテゴリ(解答)がわからないとすることもできる。このように、カテゴリ分けをできないデータの範囲のことを棄却領域(Reject Domain)という。テストの例で言えば、記憶していない問題が出されてしまったケースであり、解答をあきらめてほかの問題に時間を充てる捨て問に相当するものだろう。相場分析やテクニカル分析でも”わからない、ポジションを取らない”という選択肢があるモデルを用いることは相応に重要であると考えられる。

　最近傍法の最大の欠点はデータ量が多い場合にはメモリや計算量を非常に食うということだろう。なのでビッグデータ解析みたいなものに適用するのは難しい手法であると考えられる。また、例外的な値がたまたま最近傍値になってしまうというリスクは残ることになる。金融ではデータが多いことより少ないことの方が問題になることも少なくないので、以外に使いどころがある手法であるかもしれない。

チャートパターンの探索

　テクニカル分析における丸暗記型のパターン認識といえば、ローソク足を使ったパターン認識であり、有名なのは酒田五法だろう。三兵、三空、三山、三川、三法の５つを指しているらしい。三法はチャートのパターンではなく心構えのことらしい。外国でも似たような分析は普通にあって、三山はヘッズ・アンド・ショルダー(Heads and Shoulder)といわれている。おそらく他のものも類似の概念があるのだろう。ただ、こういうものを覚えて本当にそうなるかというとそうでもなく、三山天井っぽい動きをした後、さらに上昇していくということは普通にあるだろう。これも人間の感覚でしかなく、統計的にどうこうというのはわからないように思える。

　当然のことながら、チャートパターンは視覚的に覚える必要はなく、計算で類似のチャートを引っ張てくることができる。ただ、3日や5日程度の値動きでパターン認識をしてもあまり有意性がないものになってしまうかもしれない。ここでは、直近の一定の日数の値動き(25日,50日,100日など)について、最も近い挙動の日付を推定する方法を考える。といっても、やることは距離の定義を考えるだけである。ボラティリティの影響を排除するため、$\small n $日間の引値$ \small C_{t-1},C_{t-2},\cdots, C_{t-n} $をn日間の最高値Hと最安値Lを用いて、$$\small x_k = \frac{C_{t-k}-L}{H-L}, \quad 0 \leq x_k \leq 1$$と基準化する。このとき、過去の実績値$\small p_j $と比較する際の距離を$$\small d(x, p_j) = \sum_{k=1}^{n} \gamma_k (x_k-p_{j,k})^2 $$と定義するのが良いと考えられる(絶対値でもよいが)。ここで、$\small \gamma_k $は割引率であり、直近の値ほど重みを持たせるようにする。

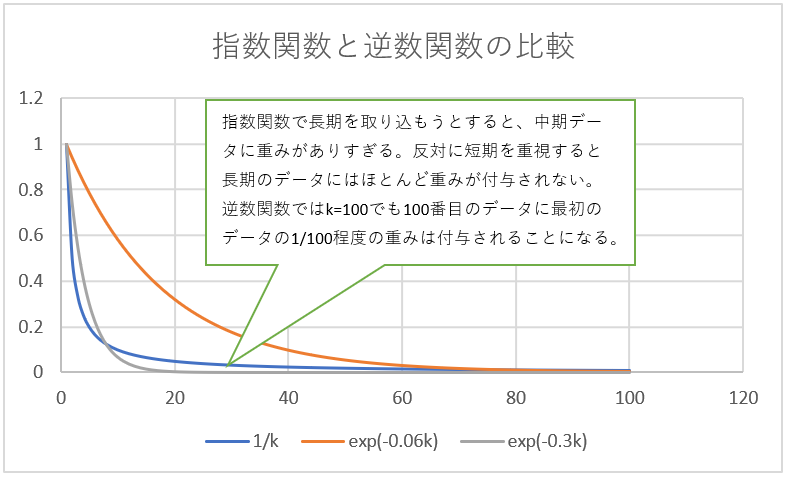
　問題は割引率$\small \gamma_k $をどう設定するかだろう。あまりに減衰が緩いと直近の動きが反映されないし、急すぎると長期のデータを見ている意味がなくなる。ディカウントファクターっぽく$ \small \gamma_k = \exp(-\delta k) $としてもよいが、減衰率$ \small \delta $をなかなかうまい具合に設定しづらい部分がある。直近をフィッティングするようにすると長期データにはほとんど重みが付与されないし、反対に長期データのパターンを取り込もうとすると短期部分が合わなくなり、現実的でないパターンが抽出されてしまうかもしれない。

　これも何となく人間のパターン認識には法則性じみたものがあるのではないかと思って、順番付けされた値に足して逆数に比例するように重みづけするという方法が使える気がしてきた。$ \small \gamma_k = \frac{1}{k} $であり、これはZipfの法則(Zipf’s Law)といわれている。指数関数と比較して手前では急速に減衰するが、後半は減衰率が低くなり長期の部分のデータも相応の重みを持つことになる。