カバーなし金利平価説の検証
金利平価説が成り立っているかを直接的に検証するのはそれほど難しいことではない。フォワードレートの式 $$\small X(t_{i}) = X(t_{i-1}) \exp((r^{2nd}(t_{i-1})- r^{1st}(t_{i-1}))(t_{i}-t_{i-1})) $$について、両辺の対数をとり、時間について積分して式を整理すると $$ \small \ln X(t_{i})=\ln X(t_{0})+\sum_{i=1}^{i-1} (r^{2nd}(t_{i-1})- r^{1st}(t_{i-1}))(t_{i}-t_{i-1})) $$と計算できる。金利差に関する感応度を測定したいので $$ \small \ln X(t_{i})=\alpha+\beta R_i+ \epsilon_i , \;\; \epsilon_i \sim N(0, \sigma^2) \quad \\ \small R_i = \sum_{i=1}^{i-1} (r^{2nd}(t_{i-1})- r^{1st}(t_{i-1}))(t_{i}-t_{i-1})) $$ という形の回帰分析の式を利用して実際のデータから推定することができる。この式で回帰分析を実行し、\( \small \beta = 1 \)が成り立つならば、金利平価説が成り立っていると考えることができる(この形ではなく、差分のまま $$ \small \ln X(t_{i})-\ln X(t_{i-1}) =\beta \dot{R}_i+ \epsilon_i , \;\; \epsilon_i \sim N(0, \sigma^2) \quad \\ \small \dot{R}_i = (r^{2nd}(t_{i-1})- r^{1st}(t_{i-1}))(t_{i}-t_{i-1})) \qquad \qquad \;\; $$ とすることもできる。為替レートの理論値みたいなのを出すために上記のようにしているだけで、基本的には等価なモデルと考えられる。)。
BISの為替レートと政策金利のデータ(1999/01/01~2021/06/30)を用いて主要な通貨について回帰分析した結果とグラフは以下のとおりである。青線が為替レート、橙線が回帰分析の結果、黄色線は\( \small \beta = 1 \)と置いた場合の推定値、灰色線が金利差を表す。金利差のみ右側の軸になっていることに注意する。
| 通貨ペア | α | β |
| AUD/USD | -0.4185 | -0.5757 |
| USD/CAD | 0.2498 | -1.3513 |
| USD/CHF | 0.5415 | 2.6087 |
| EUR/USD | 0.1933 | -1.0530 |
| GBP/USD | 0.4900 | 0.4365 |
| USD/JPY | 4.7900 | 0.4726 |
| NZD/USD | -0.6293 | -0.7471 |
| USD/NOK | 1.9646 | -0.0011 |
| USD/SEK | 2.0336 | -2.1478 |
| USD/DKK | 1.8195 | -1.9441 |
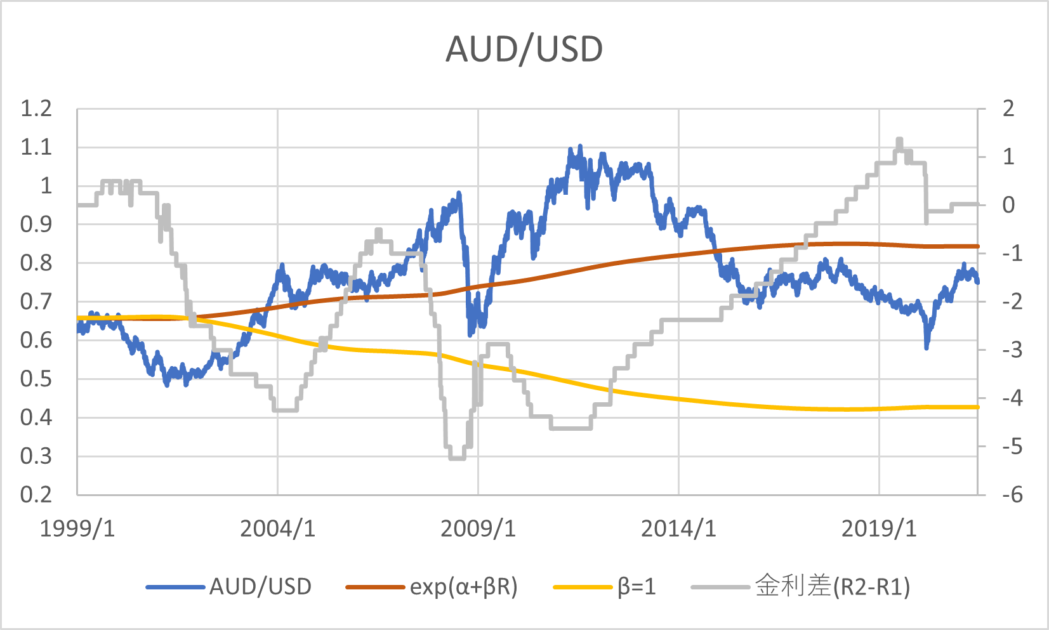
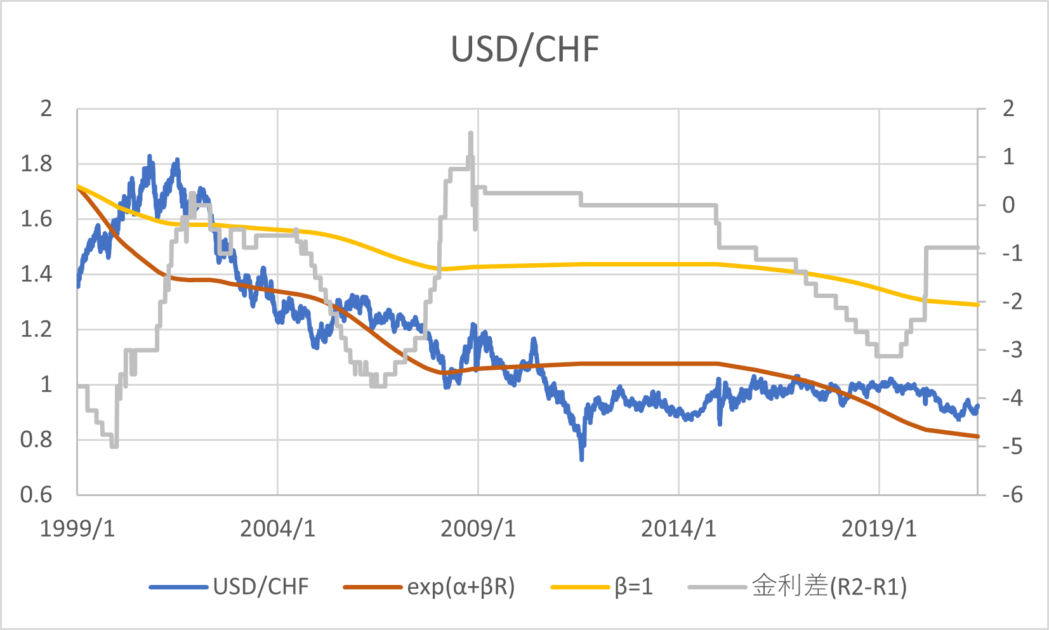
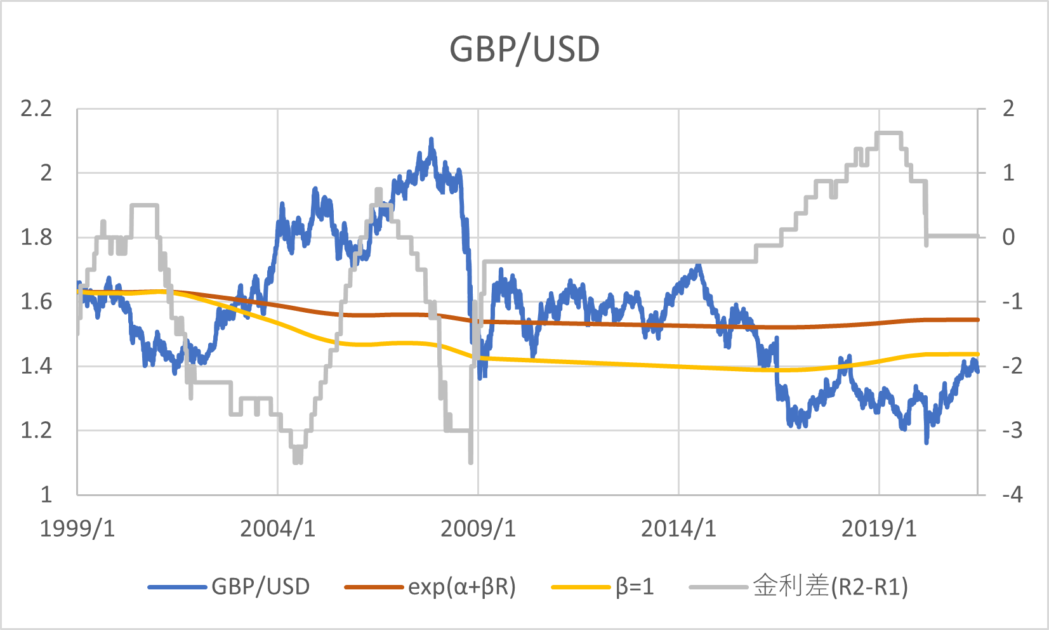
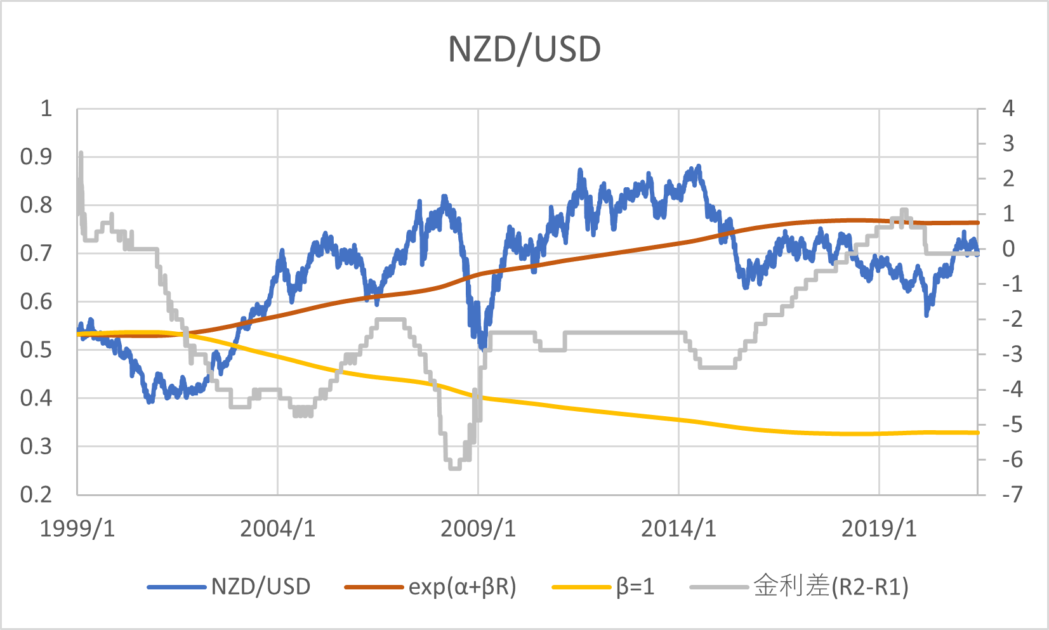
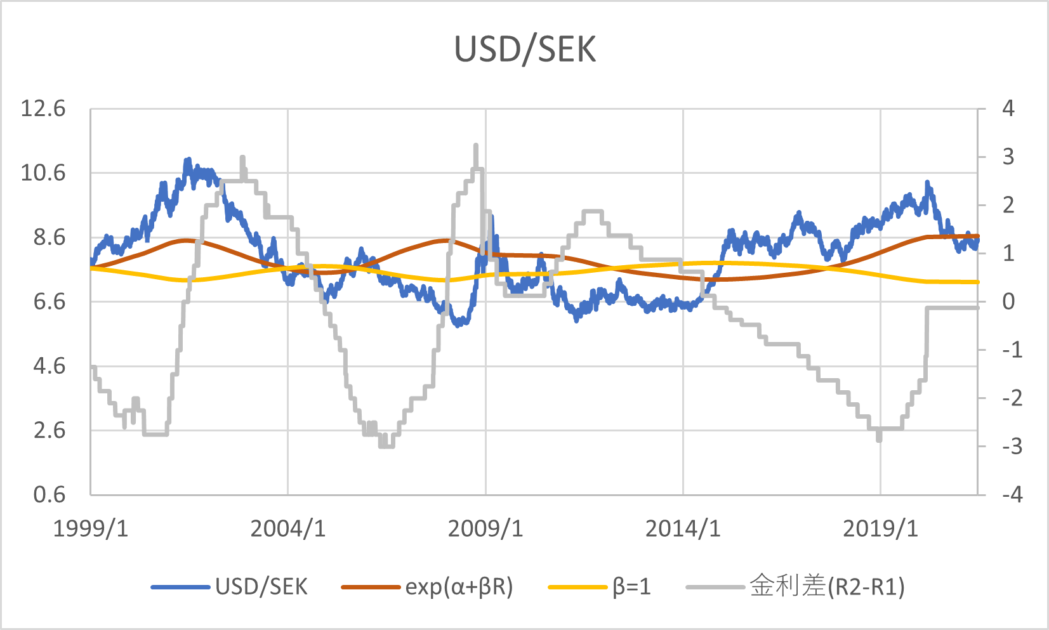
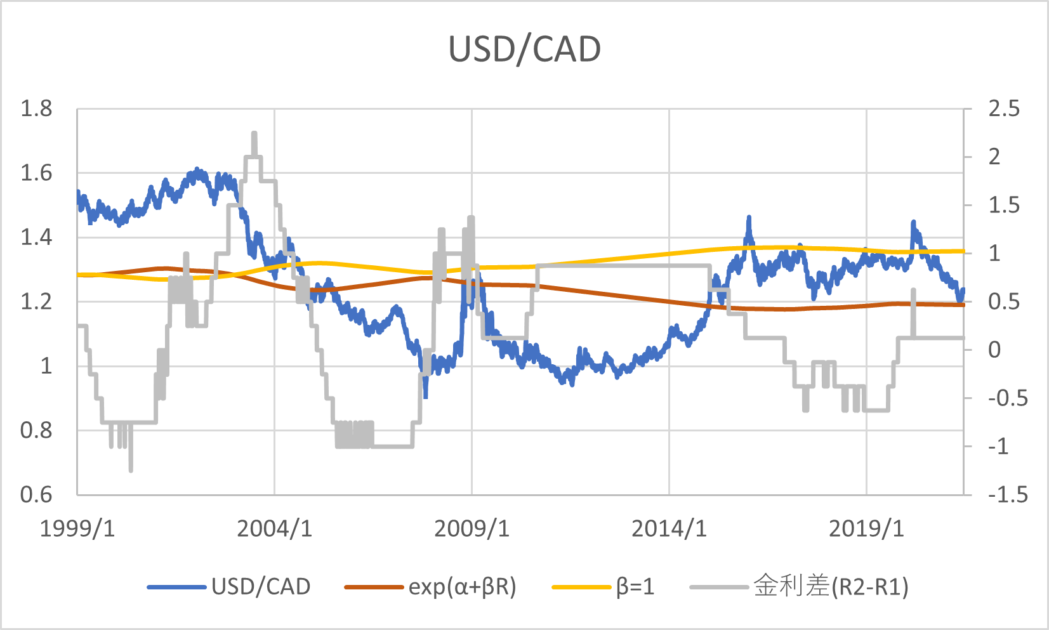
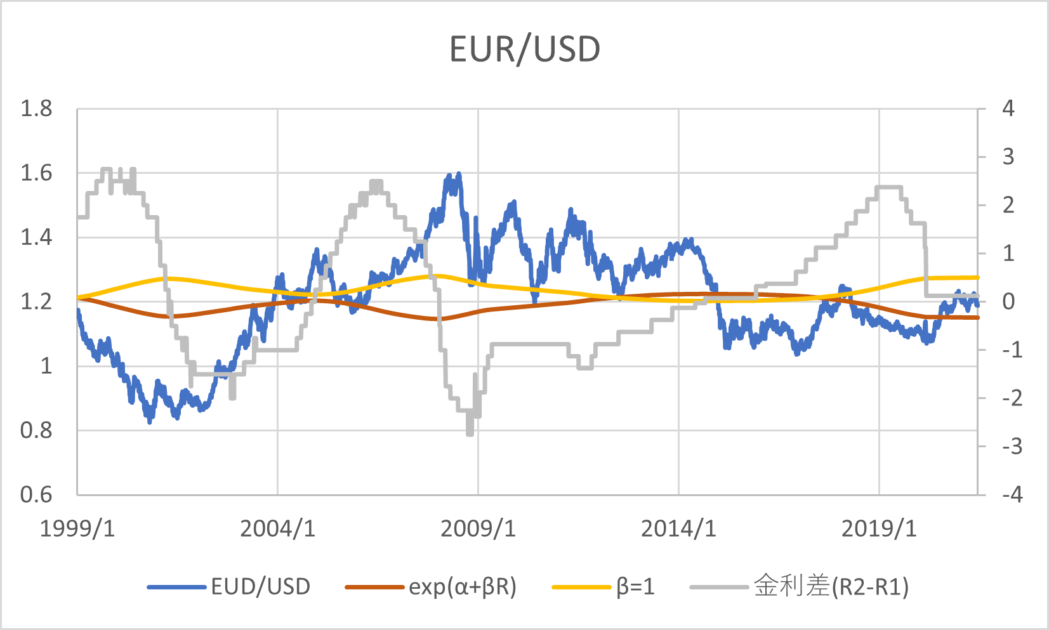
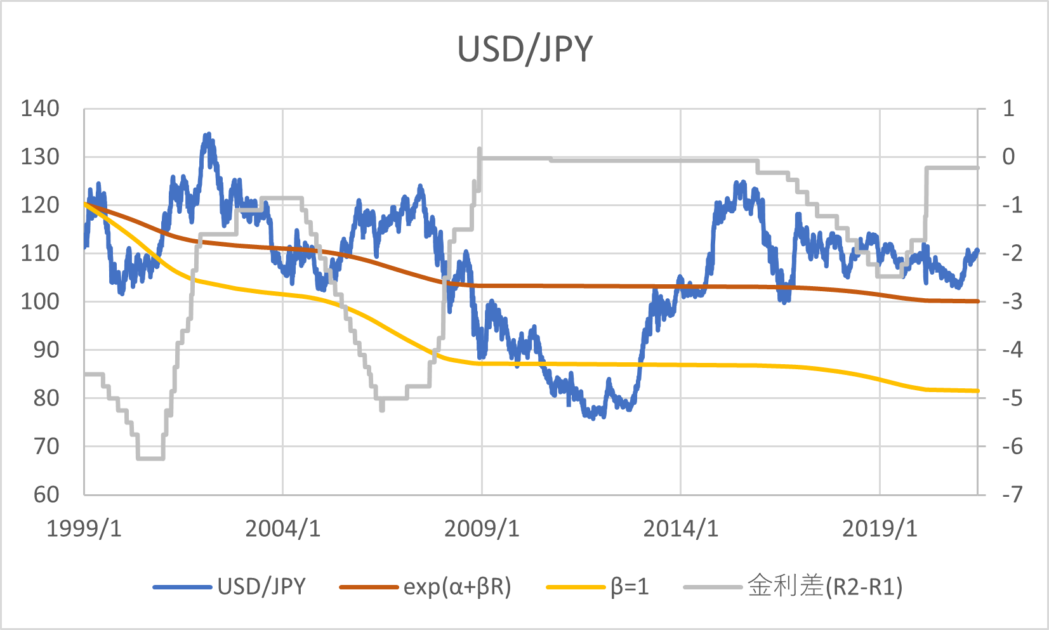
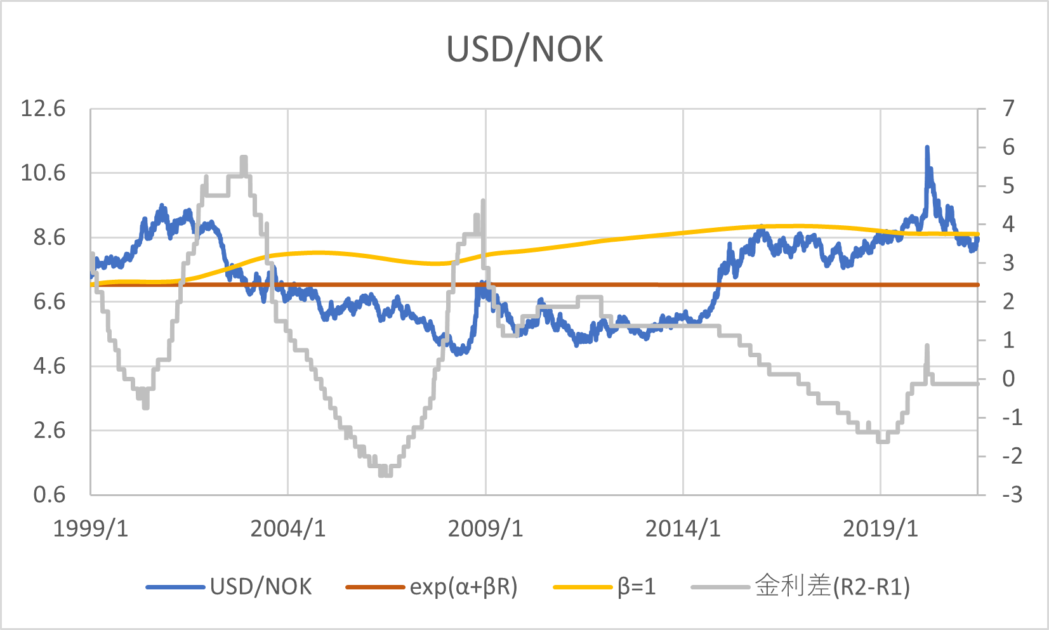
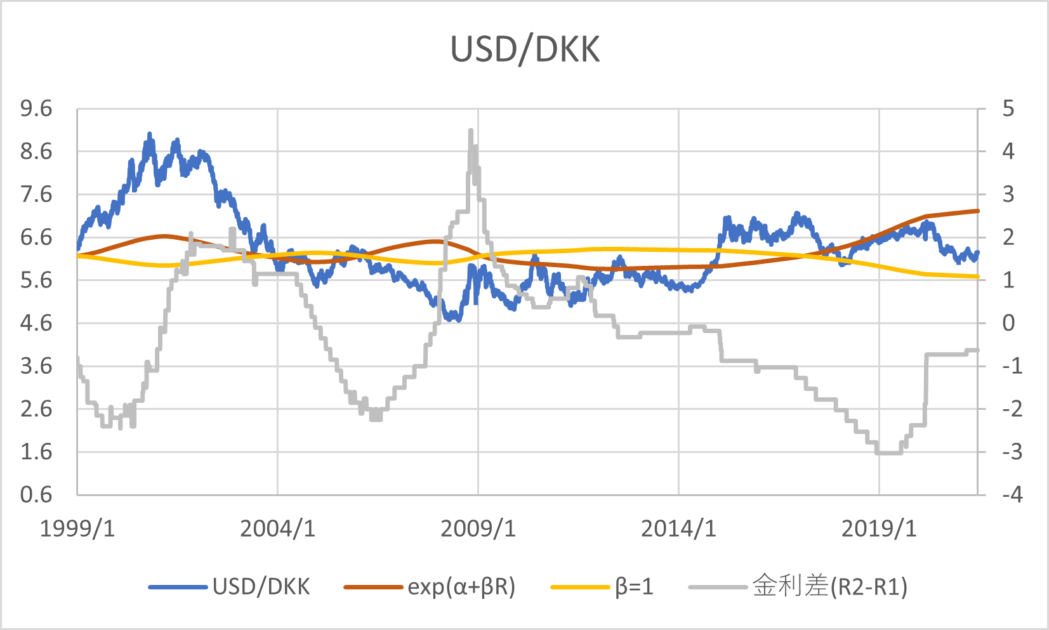
通貨の傾向として、CHF,GBP,JPYは金利平価説よりの推定値であるが1とは乖離がある数値であるといえる。AUD,NZDは金利平価説とはむしろ逆の傾向があり、キャリートレード向きの通貨であると考えることができる。その他は金利平価説が成り立たない方向に係数が算出されるが、そもそも金利水準と為替レートの水準に特定の関係性を見出すのは難しいように見える。以上のように、カバーなしの金利平価説というのは一般に成り立っているとは考えづらく、かつ、通貨によってキャリートレードの向き不向きに一定の傾向があることがわかる。